Initiation à Numpy
Les limitations des structures de données natives
Soit une liste nommée lst
>>> lst = [1, 2, 3]
>>> type(lst)
list
"Ajout" d'un entier à une liste d'entiers
>>> lst + 2
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-2-33a94180b36b> in <module>()
----> 1 l + 2
TypeError: can only concatenate list (not "int") to list
On pouvait s'attendre à avoir le résultat suivant:
[3, 4, 5]
Mais cela n'est pas le cas. Une exception TypeError est levée.
"Multiplication" d'une liste d'entiers par un entier
>>> lst = [1, 2, 3]
>>> lst * 2
[1, 2, 3, 1, 2, 3]
La liste d'origine est répétée deux fois. Alors que l'on s'attendait probablement au résultat suivant :
[2, 4, 6]
La liste d'origine n'est pas multipliée par 2 comme l'on pouvait penser.
On pourrait très bien imaginer utiliser une boucle for pour réaliser ces opérations
>>> lst = [1, 2, 3]
>>> for i, val in enumerate(lst):
>>> lst[i] = val + 2
>>> print(lst)
[3, 4, 5]
ou
>>> lst = [1, 2, 3]
>>> for i, val in enumerate(lst):
>>> lst[i] = val * 2
>>> print(lst)
[2, 4, 6]
Cela complique considérablement les choses. De plus une telle pratique s'avère généralement coûteuse en temps de calcul.
Présentation de Numpy

Afin de remédier (entre autre) à cette difficulté. La bibliothèque NumPy a été crée. Elle est écrite en langage C afin de permettre de haute perfomances.
On trouve dans le module NumPy de nombreux outils de manipulation des tableaux pour le calcul numérique.
- Nombreuses fonctions de manipulation de tableaux
- Bibliothèque mathématique importante
Il s’agit d’un module stable, bien testé et relativement bien documenté.
Pour l’importer, on recommande d’utiliser
>>> import numpy as np
Toutes les fonctions NumPy seront alors préfixées par np.
Création d'un array à partir d'une liste
>>> a = np.array([1, 2, 3])
>>> a
array([1, 2, 3])
La variable a contient désormais un array et non une list.
On parle parfois aussi en français de tableaux NumPy.
Dans notre exemple, il s'agit d'un tableau à une dimension.
Les array peuvent avoir:
- une dimension (comparable à une liste plate)
- deux dimensions (comparable à un tableau ou un matrice)
- plus de deux dimensions (cube, hypercube...)
Notion de type
>>>> type(a)
numpy.ndarray
La variable a est un Numpy Array (numpy.ndarray).
>>>> a.dtype
dtype('int64')
L'array a contient des nombres entiers (integer) codés sur 64 bits.
Ajout d'un entier à un array d'entiers
>>> a + 2
array([3, 4, 5])
Multiplication d'un array d'entiers par un entier
>>> a * 2
array([2, 4, 6])
Ce type de comportement (broadcast) est généralement plus pratique pour les scientifiques (qui ne sont pas toujours développeurs)
Quelques autres solutions pour créer un array
np.arange
>>> np.arange(4, 10, 0.5)
array([ 4. , 4.5, 5. , 5.5, 6. , 6.5, 7. , 7.5, 8. , 8.5, 9. ,
9.5])
np.linspace
>>> np.linspace(4, 10, 5)
array([ 4. , 5.5, 7. , 8.5, 10. ])
np.zeros
>>> np.zeros(5)
array([ 0., 0., 0., 0., 0.])
>>> np.zeros((2, 4))
array([[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
np.ones
>>> np.ones((2, 4))
array([[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.]])
>>> np.ones((2, 4), dtype=int)
array([[1, 1, 1, 1],
[1, 1, 1, 1]])
np.fill
>>> a = np.empty((2, 4))
>>> a.fill(5)
>>> a
array([[ 5., 5., 5., 5.],
[ 5., 5., 5., 5.]])
np.diag
>>> np.diag([1,2,3,4])
array([[1, 0, 0, 0],
[0, 2, 0, 0],
[0, 0, 3, 0],
[0, 0, 0, 4]])
Indexing
Soit un array a 2 dimensions (ligne, colonne):
>>> a = np.array([[1,2,3], [4,5,6]])
>>> a
array([[1, 2, 3],
[4, 5, 6]])
On peut obtenir la valeur présente dans ce array à la
- 2 ième ligne (i = 1)
- 3 ième colonne (j = 2)
>>> i, j = 1, 2
>>> a[i, j]
6
ou
>>> a[1, 2]
6
Attention, comme les listes, comme les chaînes de caractères, l'indice commence à 0.
On retrouve le nombre de dimensions via :
>>> a.ndim
2
La "forme" (2 lignes, 3 colonnes)
>>> a.shape
(2, 3)
La taille (nombre d'éléments)
>>> a.size
6
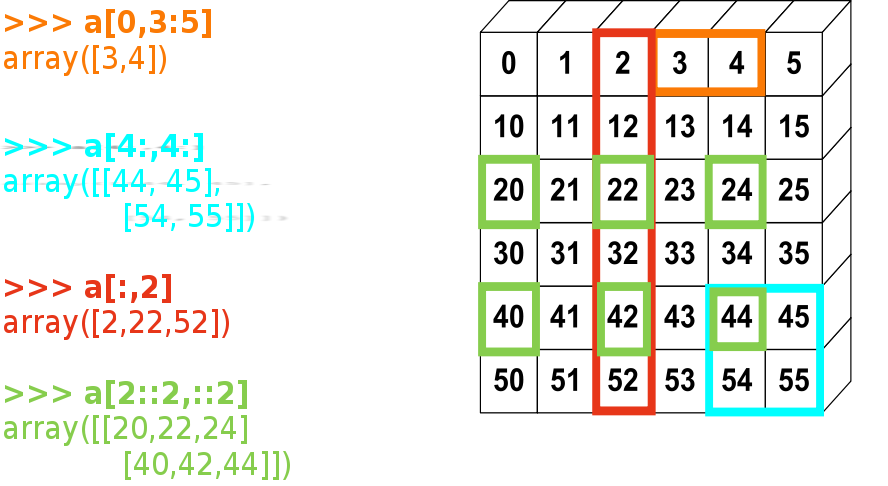
Slicing
Boolean
>>> a > 4
array([[False, False, False],
[False, True, True]], dtype=bool)
Boolean Indexing
>>> a[a > 4]
array([5, 6])
Soustraction d'array
array de même forme
>>> a = np.array([11, 12, 13, 14])
>>> b = np.array([1, 2, 3, 4])
>>> c = a - b
>>> c
[10 10 10 10]
array de forme différente (taille différente ici)
>>> a = np.array([11, 12, 13, 14])
>>> b = np.array([1, 2, 3])
>>> c = a - b
ValueError: operands could not be broadcast together with shapes (4,) (3,)
Fonctions trigonométriques
Attention si l'on fait :
>>> from math import pi, cos
>>> theta = np.array([pi, pi/2, pi/4, pi/6, 0])
>>> cos(theta)
TypeError: only length-1 arrays can be converted to Python scalars
The code below applies cosine to each of the below value to obtain the result
Il ne faut pas utiliser la fonction cos du module math si l'on veut l'appliquer
sur un array mais une version "vectorisée" appartenant à la bibliothèque NumPy
qui peut s'appliquer à tout le array.
>>> np.cos(theta)
array([ -1.00000000e+00, 6.12323400e-17, 7.07106781e-01,
8.66025404e-01, 1.00000000e+00])
Matrices
Définition avec des arrays
Soit deux matrices M1 et M2 stockées dans des arrays:
>>> M1 = np.array([[1,2],[3,4]])
>>> M1
array([[1, 2],
[3, 4]])
>>> M2 = np.array([[0,4],[0,2]])
array([[0, 4],
[0, 2]])
Le symbole * représente la multiplication terme à terme
(et non la multiplication matricielle)
La fonction dot permet d'effectuer la multiplication matricielle.
>>> np.dot(M1, M2)
array([[ 0, 8],
[ 0, 20]])
Remarque : la PEP 0465 (Python Enhancement Proposals) - A dedicated infix operator for matrix multiplication https://www.python.org/dev/peps/pep-0465/ définit @ comme opérateur de multiplication
matricielle (à partir de Python 3.5)
Définition avec des matrix
Afin d'éviter cette difficulté et afin de faciliter l'écriture,
il est possible de définir des matrices (type matrix)
>>> M1 = np.matrix([[1,2],[3,4]])
>>> M2 = np.matrix([[0,4],[0,2]])
>>> M1*M2
matrix([[ 0, 8],
[ 0, 20]])
Le symbole * est alors bien une multiplication au sens matriciel.
La transposition s'effectue via .T
>>> M1.T
matrix([[1, 3],
[2, 4]])
L'inversion via **-1
>>> M1**-1
matrix([[-2. , 1. ],
[ 1.5, -0.5]])
Diagonale d'une matrice
>>> M1.diagonal()
matrix([[1, 4]])
Trace d'un matrice (somme des coefficients diagonaux)
>>> M1.trace()
matrix([[5]])
Autres opérations utiles sur les arrays (et les matrices)
Modification de la forme
La modification de la forme (nombre de lignes, nombre de colonnes ici) en modifiant
la valeur de la propriété shape
>>> a = np.array([[1,2,3], [4,5,6]])
>>> a
array([[1, 2, 3],
[4, 5, 6]])
>>> a.shape = (3,2)
>>> a
array([[1, 2],
[3, 4],
[5, 6]])
Aplatissement
>>> a.ravel()
array([1, 2, 3, 4, 5, 6])